
https://www.acmicpc.net/problem/2749
2749번: 피보나치 수 3
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
문제 접근
문제에 대한 알고리즘을 생각하기 전에 우선 입력과 출력에 대해 관찰을 하자. 입력 값 n의 경우 범위가 조 단위가 넘어간다. 피보나치 수의 공식을 사용해서 F1부터 Fn까지 구하려고 하면 시간 복잡도가 너무 크다. 두 번째 출력에서 뜬금 없이 100만으로 나눈다고 되어 있다. 이를 활용해서 시간 복잡도를 줄일 수 있지 않을까 라고 생각 할 수 있다. 처음에는 이를 고려하지 않고 다음과 같이 막무가내로 풀었다.
#시간 초과
F = [0,1]
n = int(input())
for i in range(2,n+1):
tmp = F[1]
F[1] = F[1] + F[0]
F[0] = tmp
print(F[-1] % 1000000)당연히 시간초과가 뜨고 그제서야 문제를 앞서 언급한 부분들을 보았다. 그러나 해당 문제는 예리한 관찰력이 있더라도 사전 지식이 어느정도 있어야 수월하게 풀 수 있다.
피사노 주기
간단히 말해 피보나치의 수를 어떤 수 K로 나눈 나머지(mod K)는 일정한 주기를 가지며 이를 피사노 주기라고 한다. 문제에서 언급한 n=17까지의 수를 4로 한번 나누어 나머지를 구해보자

여기서 주기는 1 1 2 3 1 0으로 길이는 6이다. 이때, 주기의 길이를 P라고 하면 N번째 피보나치 수를 M으로 나눈 나머지는 N%번째 피보나치 수를 M으로 나눈 나머지와 같다.

그리고 나누는 수 M이 10의 제곱수인 경우 주기 P는 다음과 같은 성질을 띤다
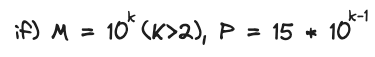
이를 활용하여 코드를 작성하면 다음과 같이 된다
문제 풀이
n = int(input())
a, b = 0, 1
n = n % (15 * (10**5)) #나누는 수 M이 10의 6제곱이니까
for i in range(n):
a, b = b % (10**6), (a+b) % (10**6)
print(a)'알고리즘_파이썬' 카테고리의 다른 글
| 백준 5073 삼각형과 세변 (0) | 2024.01.31 |
|---|---|
| 백준 9655 돌 게임 (0) | 2024.01.31 |
| 백준 2231 분해합 (1) | 2024.01.27 |
| 백준 1655 가운데를 말해요 (1) | 2024.01.24 |
| 백준 1874 스택 수열 (1) | 2024.01.23 |



